Not long into my flying I mentioned to my CFI that had gone pretty far into my ground studies long before I started flying with him. A lot had fallen out of my head apparently. When he asked me about induced drag I got my terms mixed up and confused it at first with parasitic drag (thinking it was the drag caused, i.e. induced, by the speed of the aircraft, then wondering if it was the drag caused [induced] by the form of the aircraft. Nope, forgetful me, it is the rearward component of lift. More specifically, induced drag is the component of life acting parallel to the free-stream airflow.
All is fine until I got to this topic in the Sporty’s flight training. I was expecting as simple a definition that I had come across, but it said something that seemed odd. “The wingtip vortex… is the source of induced drag and is not the same as the downwash needed to produce lift.” But wait, if the air is being deflected downward, i.e. downwash, by the creation of lift, then the relative wind is not horizontal (in straight and level flight) but at an angle, and the lift vector is pointed rearward, so there is a horizontal component to that vector and it is induced drag, right? When I go look up the definition of induced drag I get simply this: “Induced drag is the inevitable consequence of lift.” That sentence is actually alarmingly unhelpful when trying to understand just what is going on, but it directly contradicts Sporty’s definition of induced drag. Sporty’s would seem to suggest that if there is no wingtip vortex, then there is no induced drag.
Now contrast this with Wikipedia’s caption of the free body diagram. “Induced drag is related to the amount of induced downwash in the vicinity of the wing.” Right away this contradicts Sproty’s definition. Wikipedia goes on to say that the resulting downwash in the vicinity of the wing results in an effective relative airflow in a different direction than the relative free-stream airflow. So your plane is flying along in straight and level flight (with some kind of angle of attack), the relative wind is coming straight towards the airplane. However, in the vicinity of the wing the relative wind is has an induced downwash. Meanwhile the lift vector of the wing is not straight up, opposing gravity, but rather, tilted backward by the same angle between the wind near the wind and the free-stream wind. The cosine of that angle multiplied by the lift force is the induced drag force.

Wikipedia does go on to explain the reason for wingtip vortices. There is a span-wise airflow from the lower surface wing root around the wingtip back towards the upper surface wing root. This span-wise flow combines with the chord-wise flow to create vortices. The vortices are what cause the down-wash. So I’m very suspicious of Sporty’s explanation, “induced drag is not the same as downwash needed to produce lift.” Right away I have to wonder, does that mean that downwash is more pronounced at the wing tips than the wing root if the downwash is indeed induced by the vortex since the vortex would not expand all the way along the wing. Looking at the rather simplistic explanation at NASA’s website this appears to be the case. Also this article agrees with the Wikipedia article. The part that is easy to miss though is that the wingtip vortices cause an additional downwash, not all of it.


One way to explain this is Newton’s Third Law. The downward flow of the air is the equal and opposite reaction to the lifting force. So then, what were to happen if the wing were infinitely long, or if one were to totally fence off the wingtip so that there could be no spill over the wingtip, back to Wikipedia on this one: “…a wing of infinite aspect ratio and constant airfoil section would produce no induced drag. The characteristics of such a wing can be measured on a section of wing spanning the width of a wind tunnel.” So does that mean an infinitely long wing generates no lift? Is there no downwash for such a wing? Back to being confused?
MIT has lecture notes relating to this particular topic. “There is a non-zero downwash velocity -w at the wing itself (w is positive up). In other words, the wing operates in its own downwash. The apparent freestream velocity which the wing sees (compared to the airplane) is therefore tilted by the induced angle αi . The effective angle of attack that the 3-D wing sees is significantly reduced from the geometric angle of attack α; αeff = α – αi Because αeff < α, the lift generated be the 3-D wing is less than if the downwash and induced angle were absent, as in the 2-D case. In practice, this means that the 3-D wing has to operate at a greater geometric α to achieve the same lift/span as the 2-D wing.”
Maybe all of this is academic since there is no such thing as a 2-D wing. It is interesting though that there is in fact an apparent updraft ahead of the 3-D wing and downwash behind it. It is this 3-D wing that generates vortices. Induced drag is the effect of the 3-dimensional flow of air as lift is generated. I think I’m starting to get this. In the end, what was listed in the Sporty’s course seems to disagree with everything else I’ve read on the subject. Vortices make induced lift worse, but the downwash created by the 3-D wing is necessary to generate lift, and the by product of generating lift is both induced drag and downwash – penalties that simply cannot be separated, but they can be minimized.
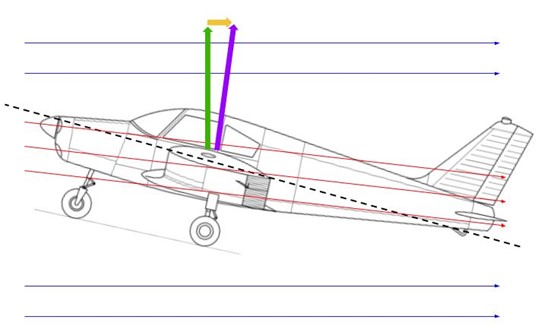
For our airplane in straight and level flight, the blue arrows represent the free-stream air not affected by the wings. The red arrows represent the flow of air deflected downward by the creation of lift. The effective lift, purple arrow, has two components, the upward component opposing gravity (green) and the induced drag component (yellow). This vector picture is with respect to the airplane, not the wing alone – the wing actis in its own downwash – the air near the wing is at a different direction than the broader free-stream air. The angle of attack of the wing is between the chord line and the red arrows, not the blue. Of course, I’ve exaggerated the downwash quite a bit, and the difference is actually not all that large.
If you want to geek out on this as much as I did, here are a bunch of things that came up in my search. If not, then just remember that induced drag is the yellow arrow!
https://howthingsfly.si.edu/ask-an-explainer/what-downwash
http://hyperphysics.phy-astr.gsu.edu/hbase/Fluids/airfoil.html
http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html#airf
http://hyperphysics.phy-astr.gsu.edu/hbase/Fluids/airfoil.html
http://hyperphysics.phy-astr.gsu.edu/hbase/Fluids/kutta.html#c1
https://en.wikipedia.org/wiki/Lift_(force)
https://en.wikipedia.org/wiki/Lifting-line_theory
https://en.wikipedia.org/wiki/Horseshoe_vortex
https://en.wikipedia.org/wiki/Wingtip_vortices
http://web.mit.edu/16.unified/www/SPRING/fluids/Spring2008/LectureNotes/f05.pdf